Оценка эффективности инвестиций, инвестиционного портфеля, акций на примере в Excel

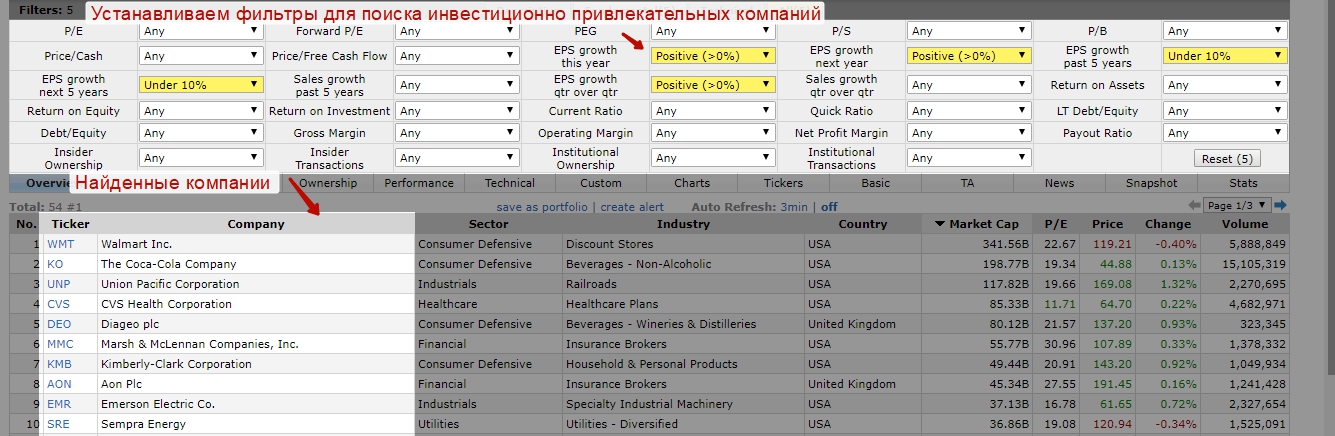
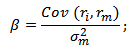Разберем: как проводится оценка акций, инвестиционных портфелей, паевых инвестиционных фондов и инвестиционных стратегий. Рассмотрим на практическом примере с использованием программы Excel как можно самостоятельно провести анализ акций и оценить эффективность инвестиций (инвестиционных портфелей). Предметом оценки эффективности управления выступают инвестиции, под которыми понимается широкий пласт различных производных финансовых инструментов: акции, облигации, фьючерсы, инвестиционные портфели, паевые инвестиционные фонды, хеджевые фонды, а также инвестиционные стратегии на фондовом рынке.

Инфографика: Оценка эффективности инвестиций, инвестиционного портфеля, акций

Показатели эффективности инвестиций на фондовом рынке

Для оценки инвестиций на фондовом рынке используют различные коэффициенты эффективности управления, которые можно разделить на две группы: абсолютные показатели эффективности инвестиций и относительные. Так абсолютные показатели эффективности инвестиций отражают абсолютные изменения ключевых показателей риска и доходности. Относительные коэффициенты показывают относительное изменение. В инвестиционном анализе доходность и риск являются ключевыми параметрами оценки любой инвестиции. В таблице ниже приводится классификация коэффициентов по различным группам: типу показателя и характеру оценки.

★ Инвестиционная оценка в Excel. Расчет NPV, IRR, DPP, PI за 5 минут

Коэффициенты	Тип показателя	Характер оценки
		Относительные	Абсолютные
Среднеарифметическая доходность	Доходность		+
Стандартное отклонение	Риск		+
Коэффициент Шарпа	Доходность/Риск	+
Коэффициент Трейнора	Доходность/Риск	+
Коэффициент Бета	Риск	+
Коэффициент Альфа Йенсена	Доходность		+
Коэффициент Модильяни	Доходность/Риск	+

Цель оценки эффективности инвестиций является определение успешных и результативных стратегий управления на фондовом рынке, которые позволяют получать доходность выше среднерыночной при минимальном уровне риска. Данные показатели используется для ранжирования и сопоставления между результатов управления портфелями. На основе коэффициентов принимаются дальнейшие решение об использовании стратегии и ее модификациях.

★ Excel таблица для формирования инвестиционного портфеля ценных бумаг (рассчитай портфель за 1 минуту) + оценка риска и доходности

Доходность инвестиций. Оценка и анализ акций

Первый один из самых важных показателей инвестиции (акции, облигации, фьючерса и т.д.) является ее доходность. Она отражает привлекательность финансового инструмента для инвесторов. Для примера мы будем оценивать доходность акции. Так чем выше привлекательность акции, тем выше ее доходность и стоимость на фондовом рынке. Для того чтобы оценить доходность акций воспользуемся сервисом сайта finam.ru, который позволяет получить текущие котировки акций в режиме реального времени.

Пример оценки доходности акций ОАО «Газпром» в Excel

Рассмотрим оценку доходности акции ОАО «Газпром» (GAZP) в Excel. Были загружены недельные котировки за 31.01.2014 – 31.01.2015 г. Далее необходимо вставить котировки акций в таблицу, как представлено на рисунке ниже.

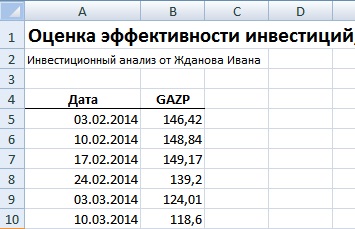
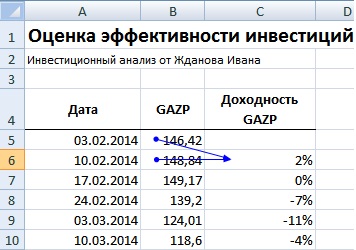
Для расчета доходности акции можно воспользоваться следующей формулой:

Доходность ОАО «Газпром» = (B6-B5)/B5

Второй вариант расчета доходности акции производится с помощью натурального логарифма доходностей. Расчет по данной формуле будет иметь аналогичный итоговый результат:

Доходность ОАО «Газпром»  =LN(B6/B5)

Прогнозирование доходности акции

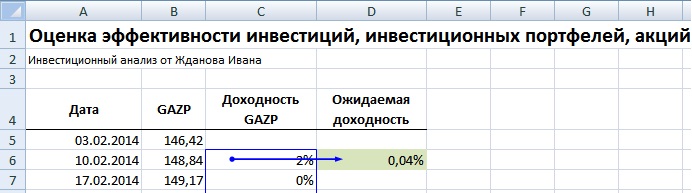
Одним из самых простых способов прогнозирования доходности акций является использование математического ожидания. Для оценки будущей (ожидаемой) доходности акции используют среднеарифметическое значение прошлых доходностей.

На рисунке ниже показан результат расчета будущей доходности ОАО «Газпром» по данной модели. Формула оценки доходности будет следующая:

Доходность акции ОАО «Газпром»  =СРЗНАЧ(C6:C56)

Оценка риска акции в Excel

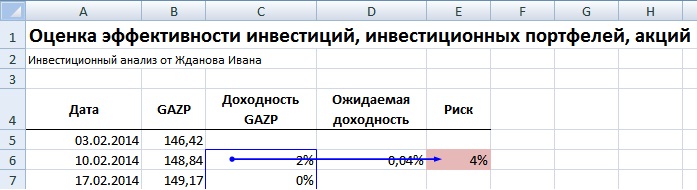
Под риском акции подразумевается его волатильность или изменчивость (данную трактовку ввел Г.Марковиц). То есть чем больше чувствительность изменения котировок, тем выше риск акции. Для расчета риска необходимо рассчитать стандартное отклонение доходностей акции от среднего. На рисунке ниже представлена формула расчета стандартного отклонения доходностей акции ОАО «Газпром».

Оценка риска акции ОАО «Газпром» =СТАНДОТКЛОН(C6:C56)

Оценка эффективности инвестиций. Коэффициент Шарпа

Коэффициент Шарпа (англ. Sharp ratio) – самый распространенный коэффициент оценки эффективности инвестиций на фондовом рынке, был введен экономистом У. Шарпом в 1966г. Данный коэффициент используют для анализа акций, фьючерсов, инвестиционных портфелей, стратегий. Коэффициент Шарпа показывает отношение доходности к риску инвестиции.

Формула расчета коэффициента Шарпа

Формула расчета коэффициента Шарпа следующая:

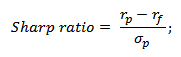где:

r_p – средняя доходность инвестиционного портфеля;

r_f – средняя доходность безрискового актива;

σ_p – стандартное отклонение доходностей инвестиционного портфеля (риск портфеля).

Как видно, коэффициент Шарпа показывает отношение избыточной доходности инвестиционного портфеля к риску. За безрисковую доходность по активу, на практике, берут:

• Доходность по банковскому вкладу наиболее надежных банков РФ;
• Доходность государственных ценных бумаг (ГКО, ОФЗ);
• Размер ключевой ставки ЦБ РФ;

Экономический смысл заключается в том, что инвестору необходимо получить доходность выше, чем минимальный уровень иначе инвестиция не имеет смысла, поэтому происходит сравнение полученной доходности инвестиционного портфеля и безрисковой процентной ставки.

★ Программа InvestRatio — расчет всех инвестиционных коэффициентов в Excel за 5 минут (расчет коэффициентов Шарпа, Сортино, Трейнора, Калмара, Модильянки бета, VaR) + прогнозирование движения курса

Оценка эффективности инвестиций по коэффициенту Шарпа

Рассмотрим более подробно анализ коэффициента Шарпа, чем выше значение показателя, тем более эффективно управляется инвестиционный портфель, тем более инвестционно привлекателен финансовый инструмент. В таблице ниже раскрывается анализ инвестиций на основе показателя Шарпа в зависимости от его значения.

Значение коэффициента Шарпа	Оценка эффективности инвестиции
Sharp ratio >1	Высокая степень эффективности управления инвестиционным портфелем, инвестициями
1>Sharp ratio >0	Уровень риска вложения в данную инвестицию выше, чем ожидаемый уровень доходности
Sharp ratio <0	Вложение не целесообразно, так как доходность безрискового актива выше

Пример расчета коэффициента Шарпа для оценки эффективности инвестиционного портфеля в Excel

Рассчитаем показатель Шарпа для инвестиционного портфеля. Для этого необходимо знать доходность по инвестиционному портфеля за определенный интервал времени. В данном примере рассматривался расчет для инвестиционного портфеля за период с 10.02.2014 по 17.03.2014 года по неделям.  Формулы расчета следующие:

Средняя доходность инвестиционного портфеля =СРЗНАЧ(B5:B10)

Риск инвестиционного портфеля  =СТАНДОТКЛОН(B5:B10)

Доходность безрискового актива = 15%/50.  Данное значение соответствует средней доходности по банковскому вкладу (15%), поделенное на количество недель в году.

Коэффициент Шарпа =(C5-E5)/D5

На рисунке ниже представлены результаты расчета.

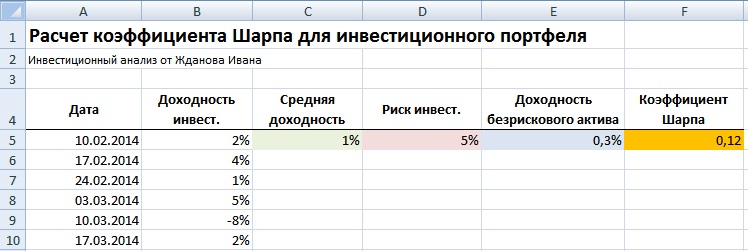
Коэффициент Шарпа составил 0,12 – это говорит о том, что данный портфель управляется довольно рискованно, то есть уровень риска выше, чем уровень доходности.

Коэффициент бета для оценки эффективности инвестиций

Коэффициент бета (англ. beta coefficient) ­– показывает чувствительность изменения доходности инвестиционного портфеля от доходности рынка (рыночного индекса). Данный коэффициент используется как самостоятельно, так и в модели оценки капитальных активов CAPM (Capital Assets Price Model).  Коэффициент бета отражает систематический риск инвестиции.

Формула расчета коэффициента бета

где:

β – коэффициент бета;

r_p – доходность инвестиционного портфеля;

r_m – рыночная доходность;

σ²_m – дисперсия рыночной доходности.

Оценка эффективности инвестиций по коэффициенту бета

В таблице ниже показан пример анализа по коэффициенту бета инвестиции на фондовом рынке. Чем выше значение показателя, тем выше возможная доходность, но в тоже время и выше риск. Для каждого типа инвесторов подходит свое значение беты. Знак коэффициента отражает направление изменения доходности инвестиции. Положительное значение беты показывает однонаправленное изменение доходности рынка и инвестиционного портфеля, отрицательное наоборот противоположное направление.

Значение показателя	Уровень риска акции	Стратегия инвестора
β > 1    β <-1	Высокий	Агрессивная
β = 1    β=-1	Умеренный	Пассивная
-1 < β < 1	Низкий	Консервативная

Оценка риска акций. Пример расчета коэффициента Бета в Excel

Для расчета коэффициента бета необходимо рассчитать ковариацию между доходностями инвестиционного портфеля и доходностями рыночного индекса (индекса РТС) и соотнести с дисперсией доходности рынка. Формула в Excel расчета следующая:

Коэффициент Бета =КОВАР(B5:B10;C5:C10)/ДИСП(C5:C10)

 

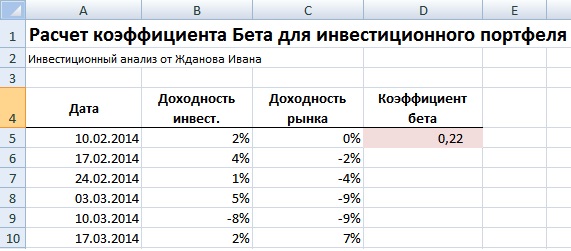
Коэффициент бета равен 0,22 – что показывает умеренный уровень рыночного риска для данного инвестиционного портфеля.

Коэффициент Трейнора для оценки эффективности инвестиций

Коэффициент Трейнора (англ. Treynor ratio) – показатель эффективности инвестиции (инвестиционного портфеля), который показывает отношение превышение доходности инвестиции над систематическим риском  портфеля. В качестве систематического риска используют значение рыночного риска, который рассчитывается как коэффициент бета. Коэффициент бета отражает чувствительность изменения доходности инвестиций и доходности рынка (рыночного индекса). Показатель Трейнора используется многими инвестиционными компаниями для осуществления ранжирования качества управления финансовыми продуктами.

Коэффициент Трейнора. Формула расчета

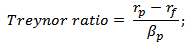
где:

r_p – средняя доходность инвестиционного портфеля;

r_f – средняя доходность безрискового актива;

β_p – рыночный риск инвестиционного портфеля.

Формула расчета коэффициента бета следующая:

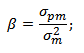где:

σ_pm – ковариация между доходностью инвестиционного портфеля и доходностью рынка;

σ²_m – дисперсия доходности рынка.

Оценка эффективности инвестиций на основе коэффициента Трейнора

Данный показатель отражает отношение между превышением доходности инвестиционного портфеля и рыночным риском данного портфеля. Чем выше значение данного показателя, тем более результативно было управление инвестициями.

Значение коэффициента Трейнора	Оценка эффективности инвестиции
Treynor ratio >0	Высокая степень эффективности управления инвестиционным портфелем, инвестициями
Treynor ratio <0	Необходимо пересмотреть стратегию управления инвестициями, так как доходность безрискового актива выше

Пример расчета коэффициента Трейнора для оценки эффективности инвестиционного портфеля в Excel

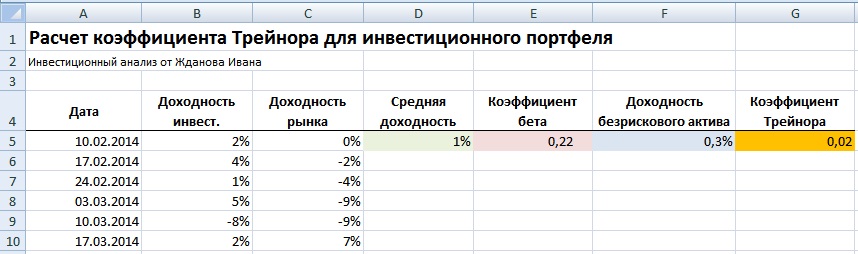
Рассмотрим на примере расчет коэффициента Трейнора для оценки результативности инвестиционного портфеля. Данные использовались аналогичные как для расчета коэффициента Шарпа, отличие заключается в использовании доходности рыночного индекса (доходность рынка). На практике, доходность рынка соответствует доходность фьючерса на индекс (RTSI). Формулы расчета коэффициента Трейнора следующие:

Средняя доходность инвестиционного портфеля =СРЗНАЧ(B5:B10)

Коэффициент бета  =КОВАР(B5:B10;C5:C10)/ДИСП(C5:C10)

Доходность безрискового актива =0,03% (Расчет аналогичен как при  расчете коэффициента Шарпа)

На рисунке ниже показан итоговый результат оценки эффективности управления портфелем. Коэффициент Трейнора составил 0,02, что рыночный риск инвестиции довольно высок, но доходность была показана выше, чем по безрисковому активу.

Коэффициент Альфа Йенсена для оценки эффективности инвестиций

Коэффициент альфа Йенсена (англ. Jensen index) – размер превышения доходности инвестиционного портфеля над среднерыночной. Данный показатель был разработан Йенсеном в 1968 году и используется для оценки эффективности управления инвестиционными портфелями. Формула расчета коэффициента Альфы Йенсена следующая:

где:

r_p – средняя доходность инвестиционного портфеля;

r_f – средняя доходность безрискового актива;

r_f – среднерыночная доходность;

β_p – рыночный риск инвестиционного портфеля.

Под среднерыночной доходностью подразумевают доходность рынка, которая равна доходности индекса РТС.

★ Программа InvestRatio — расчет всех инвестиционных коэффициентов в Excel за 5 минут (расчет коэффициентов Шарпа, Сортино, Трейнора, Калмара, Модильянки бета, VaR) + прогнозирование движения курса

Оценка инвестиционного портфеля на основе Альфы Йенсена

Чем выше значение коэффициента Альфы Йенсена, тем эффективнее активная стратегия управления на пассивной (вложение в рыночный индекс). В таблице ниже показана оценка данного показателя.

Значение коэффициента Йенсена	Оценка эффективности инвестиции
Jensen index >0	Высокая эффективность и доходность управления инвестиционным портфелем.
Jensen index <0	Низкая степень эффективности управления. Целесообразнее вложение в рыночный индекс (пассивная стратегия)

 

Пример расчета коэффициента Альфа Йенсена для оценки эффективности инвестиционного портфеля в Excel

Рассмотрим на примере расчет показателя Йенсена для инвестиционного портфеля. Данные по уровню доходности и уровням риска у нас уже есть. Формула в Excel будет иметь следующий вид:

Коэффициент Альфа Йенсена = D5-(F5+E5*(G5-F5))

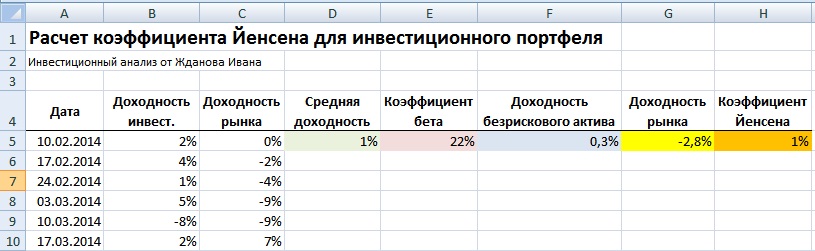
Коэффициент Йенсена составил 0,01 (1%). Так как он имеет положительное значение, это говорит об эффективном управлении портфелем и получение доходности выше среднерыночной в среднем на 1%. Активная стратегия управления инвестициями оправдывает себя.

Коэффициент Модильяни для оценки эффективности инвестиций

Коэффициент Модильяни (аналог: индекс Модильяни, коэффициент М2) – показатель отражающий эффективность управления инвестиционным портфелем. Данный показатель был предложен Франко Модильяни в 1997 г. и позволяет сравнивать между собой различные инвестиционные портфели.

Индекс Модильяни. Формула расчета

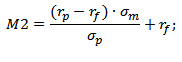
где:

r_p – средняя доходность инвестиционного портфеля;

r_f – средняя доходность безрискового актива;

β_p – рыночный риск инвестиционного портфеля;

σ_m – стандартное отклонение доходности рынка;

σ_p – стандартное отклонение доходностей инвестиционного портфеля (риск портфеля).

Оценка коэффициента Модильяни

Чем выше значение коэффициента Модильяни, тем более результативно управлялся инвестиционный портфель по отношению к бенчмарку (безрисковому активу) при соответствующем уровне риска.

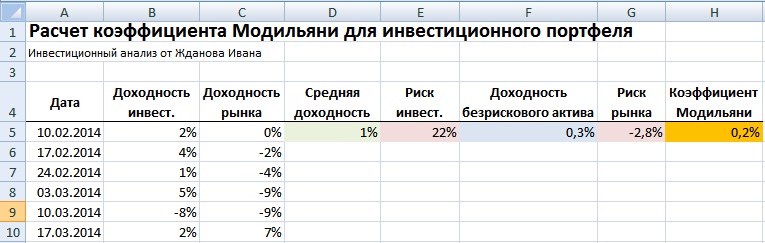
Пример расчета коэффициента Модильяни для оценки эффективности инвестиций в Excel

Для расчета коэффициента Модильяни будем использовать ранее полученные данные по доходностям инвестиционного портфеля и рынка. На рисунке ниже показан расчет коэффициента Модильяни для инвестиционного портфеля. Индекс Модильяни равен 0,2, что оценивает управление портфелем как  успешное.

 Резюме

В данной статье мы рассмотрели наиболее часто используемые показатели оценки эффективности инвестиций (инвестиционных портфелей, ПИФов и т.д.). На практическом примере рассчитали данные коэффициенты в Excel. Использование методов оценки позволяет выделить наиболее эффективные и результативные стратегии управления на фондовом рынке или пересмотреть и модифицировать уже существующие. Расчет коэффициентов позволяет минимизировать риски вложения в финансовые инструменты, применяйте их в своей инвестиционной практике.

Автор: к.э.н. Жданов Иван Юрьевич